
Biomecánica aplicada al estudio del Sistema músculo-esquelético

Dr. Carlos Arce González
Médico Especialista en Medicina de Rehabilitación
Area de Biomecánica Clínica
Lima-Perú (Enero 2005)
![]()
Generalidades
Mecánica: Parte de la Física que estudia el movimiento y equilibrio de los cuerpos (objetos materiales) y las leyes que los rigen.

|
Para su mejor estudio la Mecánica se divide en 2 partes: Dinámica y Estática.
|
M e c á n i c a | |
| Dinámica: Estudio de las leyes del movimiento de la materia. | Estática: Estudio de las leyes del equilibrio de la materia. |
|
Mecánica Dinámica | |
| Cinética: Estudio de las fuerzas que generan (modifican o detienen) el movimiento. | Cinemática: Descripción geométrica del movimiento en términos de desplazamiento, velocidad y aceleración. |
![]()
Biomecánica:
Mecánica aplicada al estudio y manejo de los procesos que afectan al sistema músculo-esquelético, aparato sustentacular u osteo-mioarticular.
Ciencia que estudia las fuerzas internas y externas, y cómo inciden éstas sobre el cuerpo humano (Hay, 1973)
Conjunto de conocimientos interdisciplinares generados a partir de utilizar, con el apoyo de otras ciencias biomédicas, los conocimientos de la mecánica y distintas tecnologías en, primero, el estudio del comportamiento de los sistemas biológicos y, en particular, del cuerpo humano y, segundo, en resolver los problemas que le provocan las distintas condiciones a las que puede verse sometido (IBV, 1992)
El análisis de los movimientos corporales (biomecánica) sigue una constante evolución, a los aspectos de orden anatómico-mecánico, se agregan los resultados de las investigaciones neuro- (electro)fisiológicas que aportan diversos parámetros que aplicados a la clínica mejoran los resultados finales.
La mecánica ortopédica se basa en la aplicación de fuerzas mecánicas – con el conocimiento de la anatomía y de la fisiología – para la prevención, corrección y tratamiento de diversos procesos patológicos que afectan al sistema musculoesquelético.
Fundamentos biomecánicos
Física: Ciencia que considera las magnitudes objeto de medida. Las leyes de la Física son el fundamento de una serie de aplicaciones prácticas de las fuerzas de la naturaleza.
Medir una magnitud física es determinar la relación existente entre la magnitud dada y otra
de su misma especie elegida (unidad)
| Unidad de longitud |
|
metro (m) |
| Unidad de masa |
|
kilogramo (Kg) |
| Unidad de tiempo |
|
segundo (s) |
| Unidad de frecuencia |
|
Hertz (Hz) |
| Unidad de fuerza |
|
Newton (N) |
Yatrofísica (Borelli, Giovanni Alfonso). Integra la fisiología y la física y, demuestra mediante métodos geométricos los diversos movimientos humanos. Obra: "On the Motion of Animals" (1680) un estudio de las bases mecánicas de la respiración, circulación y contracción muscular en animales.
|
|
|
![]()
Fuerza (F)
" Estudio de las fuerzas actuantes y/o generadas por el cuerpo humano y sobre los efectos de estas fuerzas en los
tejidos o materiales implantados en el organismo" (Sociedad Ibérica de Biomecánica, 1978).
Término referido a la tracción o empuje. Podemos ejercer una fuerza sobre un cuerpo mediante un esfuerzo muscular; un resorte tenso ejerce fuerzas sobre los cuerpos a los que está sujeto; el aire comprimido ejerce una fuerza sobre las paredes del recipiente que lo contiene.
Tipos de fuerzas:
- Fuerzas de contacto (el cuerpo que ejerce la fuerza está en contacto con el cuerpo sobre el cuál se ejerce)
- Fuerzas de acción a distancia (fuerza gravitatoria, fuerza eléctrica y fuerza magnética)
- Fuerzas exteriores (extrínsecas): Fuerzas que actúan sobre un cuerpo dado, ejercidas por otros cuerpos.
- Fuerzas interiores (intrínsecas): Fuerzas ejercidas sobre una parte de un cuerpo por otras partes del mismo.
Ecuación fundamental de la dinámica: F/a = m; se deduce
que: Fuerza (F) es el producto de la masa (m) por la
aceleración (a) F = m x a
(2da ley de
Newton)
La unidad de fuerza en el sistema C.G.S. es la Dina y en sistema M.K.S. es el Newton.
Magnitudes vectoriales
Representación gráfica de las fuerzas: Vectores.
Una fuerza (F) se representa por medio de un vector cuyo origen corresponde al punto de aplicación; la flecha indica el sentido sobre la dirección marcada por la recta.
Si una longitud de 1 cm. representa la unidad de F, una longitud de 50 cm. representará una F cincuenta veces mayor.
En toda fuerza hay que distinguir cuatro elementos:

Elementos de una Fuerza
1. Punto de aplicación Es el punto del cuerpo sobre el cuál actúa la fuerza; ejm. el punto de unión entre un coche y los arneses de un caballo. 2. Dirección Es la recta que sigue o tiende a seguir el p.a. si sólo obedece a la acción de la fuerza. 3. Sentido Una vez fijada la dirección se establecen 2 sentidos; se toman como positivas las fuerzas que actúan en un sentido y negativas las que actúan en sentido opuesto. 4. Intensidad Es la relación entre la fuerza considerada y otra tomada como unidad.
![]()
Sistema de fuerzas: Componentes y resultante
Cuando varias fuerzas actúan sobre puntos invariablemente unidos, forman lo que se llama un sistema de fuerzas. Cuando un sistema de fuerzas puede sustituirse por una sola fuerza capaz de realizar el mismo efecto, esta fuerza se denomina resultante (R).
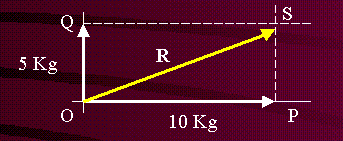
Fuerzas perpendiculares
El gráfico muestra 2 fuerzas de 5 y 10 Kg. aplicadas simultáneamente (O) La flecha OS representa la resultante de las fuerzas dadas. Su longitud, a la misma escala que la utilizada para las fuerzas dadas, determina la intensidad de la resultante, y el ángulo, su dirección.
Se deduce que, una sola fuerza de 11,2 Kg. (Teorema de Pitágoras), que forme un ángulo de 26,5° con la horizontal, producirá el mismo efecto que las 2 fuerzas de 10 y 5 Kg.
Momento de una fuerza

Barra rígida sostenida en su punto medio por la arista de una cuchilla, con un peso de 4 Kg. suspendido de un punto situado 3 m a la izquierda de la arista. Es evidente que este peso único producirá la rotación de la barra alrededor de la arista, en sentido antihorario.
Supongamos que queremos contrarrestar el efecto de rotación del peso de 4 Kg. colgando un peso de 3 Kg. en algún punto situado a la derecha de la arista. Puede comprobarse que el peso de 3 Kg. tiene que suspenderse a una distancia de la arista mayor que el peso de 4 Kg. y mediante este experimento veríamos que si se colgara exactamente a una distancia de 4 m la barra quedaría equilibrada (condición de equilibrio).
Tal experimento indica la efectividad de una fuerza para producir efectos de rotación alrededor del eje a la línea de acción de la misma. Esta distancia recibe el nombre de brazo de palanca o brazo de momento de la fuerza. Así, el brazo de momento del peso de 3Kg. es de 4 m. y el del peso de 4Kg. es de 3 m.
El momento es el producto de la fuerza aplicada por la distancia entre el punto de aplicación y el punto de rotación del cuerpo. En una palanca, la distancia entre el fulcro y el punto de aplicación de una fuerza se denomina "brazo de palanca". Así pues, el principio de la palanca afirma que una fuerza pequeña puede estar en equilibrio con una fuerza grande si la proporción entre los brazos de palanca de ambas fuerzas es la adecuada.
|
Sistema de palanca en equilibrio |
En la palanca se consideran dos fuerzas: una carga o resistencia, que suele ser el peso de un objeto que se desea mover; y una potencia, que es la fuerza que se ejerce para causar el movimiento. Este principio de la palanca se puede expresar como una sencilla ecuación:
FpBp = FrBr
Donde Fp y Fr son las fuerzas de potencia y resistencia, respectivamente; y Bp y Br sus respectivos brazos de palanca.
 |
![]()
Centro de gravedad
El peso de un cuerpo se define como la fuerza de atracción gravitatoria ejercida por la tierra sobre él.
La dirección de la fuerza gravitatoria sobre cada elemento de un cuerpo está dirigida verticalmente hacia abajo, al igual que la dirección de la resultante, independientemente de la orientación del cuerpo.
El punto fijo por el cuál pasan todas estas líneas de acción recibe el nombre de centro de gravedad corporal (baricentro). En el ser humano está localizado por delante de S2.
El baricentro está localizado en la intersección de los 3 planos corporales (Steindler-Govaers)
| Fuerza gravitatoria | Baricentro |
|
|
|
![]()
Aplicaciones clínicas
Fuerza:
La fuerza se define como la capacidad de contraer los músculos con diferentes grados de tensión c/s desplazamiento de una masa.
Tipos de contracción muscular
| Tipo |
Sinonimia |
Características |
| Isométrica | Estática | El músculo desarrolla tensión pero no cambia su longitud externa (constante). Contracción muscular sin rango de movimiento. |
| Isotónica | Dinámica | Concéntrica: El músculo se acorta, variando su tensión; mientras vence una carga constante. Sus puntos de inserción se aproximan. Contracción muscular con movimiento articular centrípeto. |
| Excéntrica: El músculo se alarga, variando su tensión; mientras vence una resistencia constante. Sus puntos de inserción se alejan. Contracción muscular con movimiento articular centrífugo. | ||
| Isoquinética | Isokinética | La tensión desarrollada durante la contracción es máxima durante todo el ROM. |
En la contracción muscular isométrica (estática) se produce un aumento de la tensión intramuscular (TIM) sin producirse movimiento articular.
En la contracción muscular isotónica (dinámica) el músculo desarrolla TIM; que puede ser de tipo concéntrica o excéntrica.
La contracción muscular isoquinética se logra con la ayuda de equipos computarizados empleados para la reeducación y entrenamiento muscular (Nautilius, Cybex, Kin-Com).
Contracción Isométrica e Isotónica (Concéntrica-Excéntrica)
![]()
Componentes del Movimiento
"La Biomecánica es la ciencia que estudia los movimientos del hombre y su coordinación" (Escuela Soviética - 1971)
El movimiento es toda acción que permite el desplazamiento desde un lugar a otro y los efectos que de ello resulte. La motricidad es la capacidad de generar movimiento.
El movimiento implica la participación del elemento comando (SNC-SNP) y el elemento efector (músculo).
El elemento anatómico encargado de producir movimiento es el aparato locomotor y se estudia desde el punto de vista biomecánico.
Se puede establecer una correlación entre las partes osteoarticulares/partes blandas y los elementos anatómicos y mecánicos. (ver tabla adjunta)
| COMPONENTES | ELEMENTOS ANATOMICOS | ELEMENTOS MECANICOS |
| Partes osteoarticulares | ||
| Huesos | Palancas | |
| Articulaciones | Charnelas - Goznes | |
| Partes blandas | Músculos | Motores |
| Tendones | Cables | |
| Ligamentos | Refuerzos - Cierres |
El suministro energético para producir el movimiento se realiza a través de la acción muscular
( "motor"). El músculo transforma la energía química en energía mecánica.
Sistema de Palancas corporales
La palanca es una máquina simple compuesta por una barra rígida que puede girar libremente alrededor de un punto de apoyo, o fulcro.
El ensamblaje del movimiento humano se realiza mediante sistemas de palancas músculo-hueso. La tensión de los músculos se aprovecha al actuar en la serie de palancas proporcionadas por los tejidos óseos rígidos. Los componentes óseos actúan como brazos de palanca y la articulaciones constituyen el eje de movimiento (fulcro); la fuerza depende de la contracción muscular.
Este complejo mecánico obedece a las leyes de las palancas, reposa en el suelo por medio de apoyos variables y está sometido a la acción de la fuerza gravitatoria y a las leyes del equilibrio.
Los huesos forman entre sí sistemas de palancas destinadas a moverse alrededor de un eje fijo, denominado punto de apoyo (A).
Los músculos constituyen la potencia (P) que mueve la palanca; sus inserciones son los puntos de aplicación de esta potencia.
La resistencia (R) está constituida por el peso del segmento a utilizar, incrementado, según el caso, por una resistencia externa (pesas, oposición) o interna (ligamentos y músculos antagonistas)
|
Video: Acción del Biceps braquial * Coloque el cursor sobre la imagen * |
||
Tipos o Géneros de palancas corporales
Las palancas pueden ser de tres géneros o tipos, dependiendo de la posición relativa del fulcro y los puntos de aplicación de las fuerzas de potencia y de resistencia. El principio de la palanca es válido indistintamente del tipo, pero el efecto y forma de uso de cada tipo de palanca cambia considerablemente.
|
Género |
Denominación |
Modelos | ||
| Primer |
|
InterApoyante | Palanca de equilibrio | Columna cervical (art. occipitoatloidea). |
| Segundo |
|
InterResistente | Palanca de fuerza | Tobillo-pie (art. tibiotarsiana) - Postura digitigrada |
| Tercer |
|
InterPotente | Palanca de velocidad | Biceps braquial |
Referencias Bibliográficas/Websites
Fucci S., Benigni M. et al.: "Biomecánica del aparato locomotor aplicada al acondicionamiento muscular".Editorial Mosby/Doyma. 1995.
Gowitzke B., Milner M.: "El cuerpo y sus movimientos - Bases científicas".Editorial Paidotribo.2001
Kapanji, J.
“Cuadernos de
Fisiología articular”. Ed. Toray Masson. 1979.
Miralles R., Puig M.: “Biomecánica clínica del aparato locomotor” . Editorial Masson, S.A. 1998.
http://www.ibv.org/ Instituto de
Biomecánica de Valencia (España). ![]()
http://www.isbweb.org/ International
Society of Biomechanics (ISB) ![]()
http://asb-biomech.org/ American
Society of Biomechanics (ASB)
![]()
![]()